ربما ما حدث مؤخراً على مختلف صفحات التواصل الاجتماعي العالمية، يُعد أمراً فريداً من نوعه كثيراً؛ فكيف من الممكن أن يكون «الجميع على حق» مهما اختلفت إجاباتهم في معادلة رياضية؟! هذا ما حدث في مسألة رياضية أثارت جدلاً واسعاً وآراءً عديدة مختلفة بشأنها بهدف الوصول إلى الإجابة الصحيحة، والغريب بكل هذا الأمر أن معظم من أجابوا عنها كانت إجاباتهم صحيحة!
ووفقاً لما نشره موقع «سكاي نيوز»، عن موقع «مشابل» العالمي، فإن هذه العملية الحسابية التي أثارت كل هذا الجدل والحيرة، هي: (2+2) 2 ÷ 8. وكان البعض قد أجاب بأن النائج هو 16، فيما قال البعض الآخر ممن حاولوا الإجابة عن المسألة، إن النتيجة هي 1 فقط. والغريب أن كليهما صحيح.
وتابع الموقع، أن الفريق الأول قال بأنه بدأ بقسمة الرقم 8 على 2، فحصل على نتيجة 4، ومن ثم قام بجمع الرقمين الموجودين بين قوسين أي 2 + 2، فجرى الحصول على 4 أيضاً. وهكذا تكون العملية الختامية هي 4X4 فيكون المجموع هو 16.
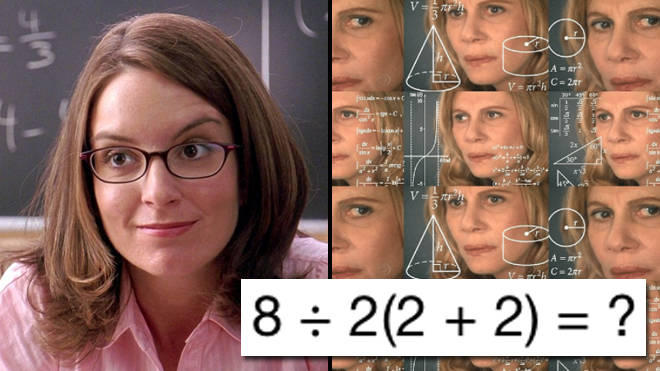
أما الفريق الثاني، فقد عمل باعتبار أن الرقم 8 معزولاً لوحده، ثم انتقل إلى الجزء الثاني من المسألة، وضرب 2 في (2+2)؛ أي 2 في 4 فتم الحصول على الرقم 8. وبعد ذلك انتقل إلى مرحلة جديدة، وقسّم الرقم 8 على 8، فكانت النتيجة 1 فقط. وهاتان النتيجتان المختلفتان تماماً للمسألة الرياضية نفسها، أثارت جدلاً وانقساماً كبيراً في آراء المعلقين عليها في التواصل الاجتماعي.
من جهته، قال موقع «مشابل» العالمي، إن الأمر الذي لم يتمكن المشاركون من إدراكه، هو أنهم جميعاً كانوا على صواب، وأن الأمر في هذه المسألة الغريبة كان يعتمد على الطريقة التي درسوا بها الرياضيات في بلدانهم، وهذا أمر أساسي في حلّها، مضيفاً أن حل هذه المادة من خلال الطريقة المعروفة بـ«بيمداس PEMDAS»، تعتمد على ترتيب خاص في حل المعادلة؛ وذلك لأن من حلوها على هذه الطريقة عادة ما يمنحون الأولوية في الحلّ للأرقام التي توجد بين قوسين. وبعد ذلك يقومون بالانتقال إلى ما يُعرف بالـ«أُس» أو الدليل، وعندها ينتلقون إلى الضرب والقسمة والجمع.
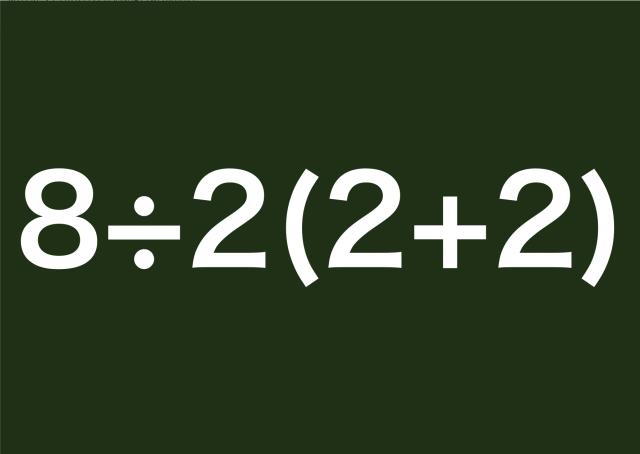
أما الفريق الآخر الذين درسوا حل المعادلات الرياضية بطريقة المعروفة بـ«بودماس BODMAS»، فالأمر يختلف معهم؛ حيث إنهم يبدأون بحل الأرقام التي توجد ما بين القوسين، قبل أن ينتقلوا إلى المرحلة الثانية من حل المعادلة ويبدأون بعمليات القسمة والضرب والجمع والطرح.





























